教科書が変わる！！～数学編～

①日常生活を意識した改訂　入試でも出題は増加！

今回の改訂では「日常生活や社会の事象を数理的に捉え、数学的に処理し、問題を解決する」ことと、「数学の事象について統合的・発展的に考え問題を解決する」ことの２つの過程を重視しています。難しいこと書かれてますね。下をご覧ください。こちらが文部科学省が示した算数・数学の学習過程のイメージです。これからもわかるように「数学の世界」だけでなく、「現実の世界」も重視することがよくわかります。今後の高校入試にも日常生活のことを数学的に取り上げた問題が増えそうですよ。

②数学なのに光の反射？他の教科の内容を数学的に扱う

新しい教科書では他の科目の内容も取り入れられています。例えば前述の鏡に映る像を相似の考え方を使って解いていくというようなものです。
具体的には社会の時差、得票率、理科のばねののび、質量パーセント濃度（食塩水の濃度）、速さなどになります。
日頃の勉強でも他の教科と関連づける意識が必要になってきますね。

③「資料の活用」が「データの活用」に！　どう変わるの？？

今回の数学の学習指導要領改訂での一番大きな変化は【資料の活用】が【データの活用】に変わることです。名前だけではなく内容も大きく変更があります。
履修学年の変更（素因数分解　中3→中1　誤差・近似値・真の値　中1→中3）や2020年度から中1で学習していた最頻値・中央値などの代表値が小６で扱われるようになりました。また、新しく【累積度数】【反例】【四分位範囲、箱ひげ図】が高校で扱われていた内容が中学校におりてきます。
単に計算や証明ができるようになるだけではなく、「思考力・判断力・表現力」を育むような作りになっています。

〇累積度数

　累積度数とは、度数分布表で最小の階級から各階級までの度数の総和を表したものです。
また、各階級の度数の、全体に対する部分の割合を相対度数といい、最小の階級から各階級までの相対度数の総和を累積相対度数といいます。
例題を見てみましょう。

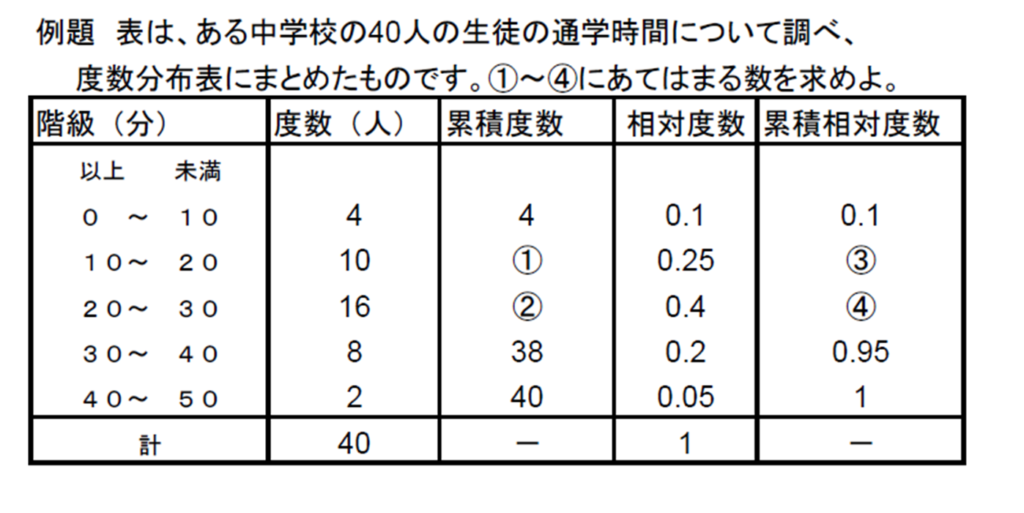
・累積度数とは、はじめ階級からその階級までの度数の総和になるので
①は４＋１０＝１４　②は４＋１０＋１６＝３０　となります。
・累積相対度数もはじめの階級からその階級までの相対度数の総和になるので
③は0.1＋0.25＝0.35　④は0.1＋0.25＋0.4＝0.75　となります。

どうです？別のやり方もありますよ！いろいろなやり方で考えてみましょう！

〇反例

　反例とは「命題の仮定を満たしているが、結論を満たしていない例」のことです。
？？ってなりますよね。では例題です。

例題　自然数nが４の倍数であり６の倍数でもあるとき、nは２４の倍数である。
　　　　　　　　　
　　自然数nが４の倍数であり６の倍数でもあるとき、nは２４の倍数である。
　　　　　　　　　　　仮定　　　　　　　　　　　　 結論
となります。ここでn=１２のとき、１２は４の倍数であり６の倍数でもあるが、24の倍数ではないことになります。仮定を満たすが結論を満たさないn=１２をこの命題の反例といいます。たくさんある事象の中からあてはまらないものを探すのは大変ですね。反例を学ぶことによって、日常生活のコミュニケーションや議論に生かそうということも考えられているみたいですよ。

〇四分位範囲・箱ひげ図

　四分位範囲とはデータの散らばりの度合いを表す値のことです。全体を４つに分けたときの中央の２区分についてデータの散らばりの度合いを調べるものになります。
　箱ひげ図はこの中央に集まる半数のデータを四角（箱）でそれ以外の部分を箱からのびた線（ひげ）で表した図になります。こんな図です。

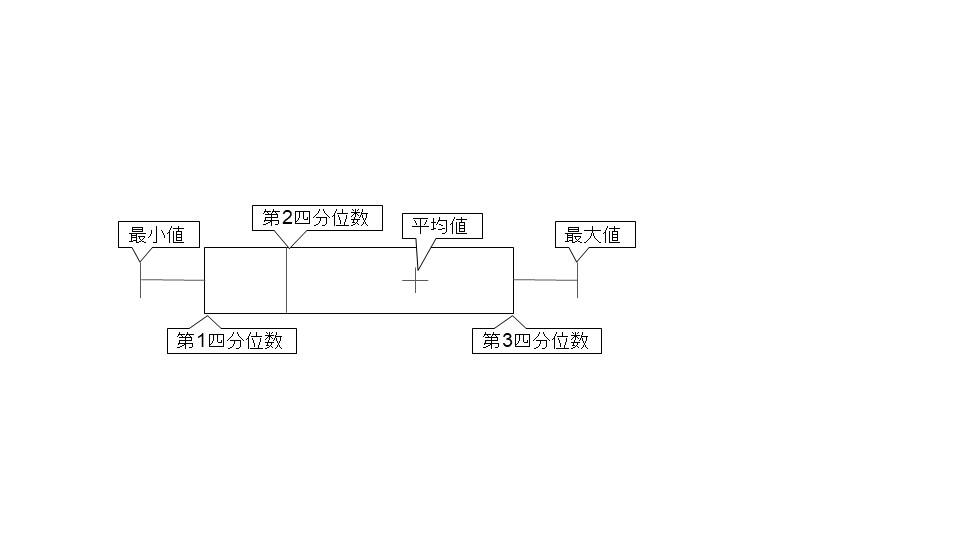
四分位範囲は第3四分位数と第1四分位数の差（箱の長さ）になります。
箱ひげ図はいろいろな分野（株価・品質管理など）で活用されています。見たことあります？？

イベント情報や学チャンの更新情報・活動の様子をSNSなどでお知らせしています!!

▼イベントの様子や学校紹介を写真でお届けします♪フォロアー対象のキャンペーンも企画中…!?

【公式Instagram】https://www.instagram.com/gakuchan_0404/

【公式Facebook】https://www.facebook.com/tanakagakushukai/

▼記事の更新情報やお友達だけが知れるイベント・キャンペーン情報をお届けします☆

【LINE公式アカウント】https://lin.ee/YzpKNGm

▼広島県内の中学校　高校のツイートを総まとめ！いろんな学校の発信をチェックしよう👀

【公式Twitter】https://twitter.com/gakushujuku